Eksponentielle funktioner
Eksponentielle funktioner har regneforskriften {$$\bf y=b \cdot\ a^x $$}
hvor a og b er konstanter, som begge er større end nul (a>0 og b>0)
Konstanten a er det tal, som y-værdien ganges med (a kaldes derfor ofte for fremskrivningsfaktoren), når x-værdien øges med 1 (se under "Vækstform" længere nede på siden). Funktionen er derfor voksende, hvis a>1, og aftagende hvis 0<a<1.
Konstanten b er y-værdien, når x=0, eller med andre ord: skæringen med y-aksen. Det ses af følgende lille udregning:
{$$ y=f(0)=b\cdot a^0=b\cdot 1=b $$}
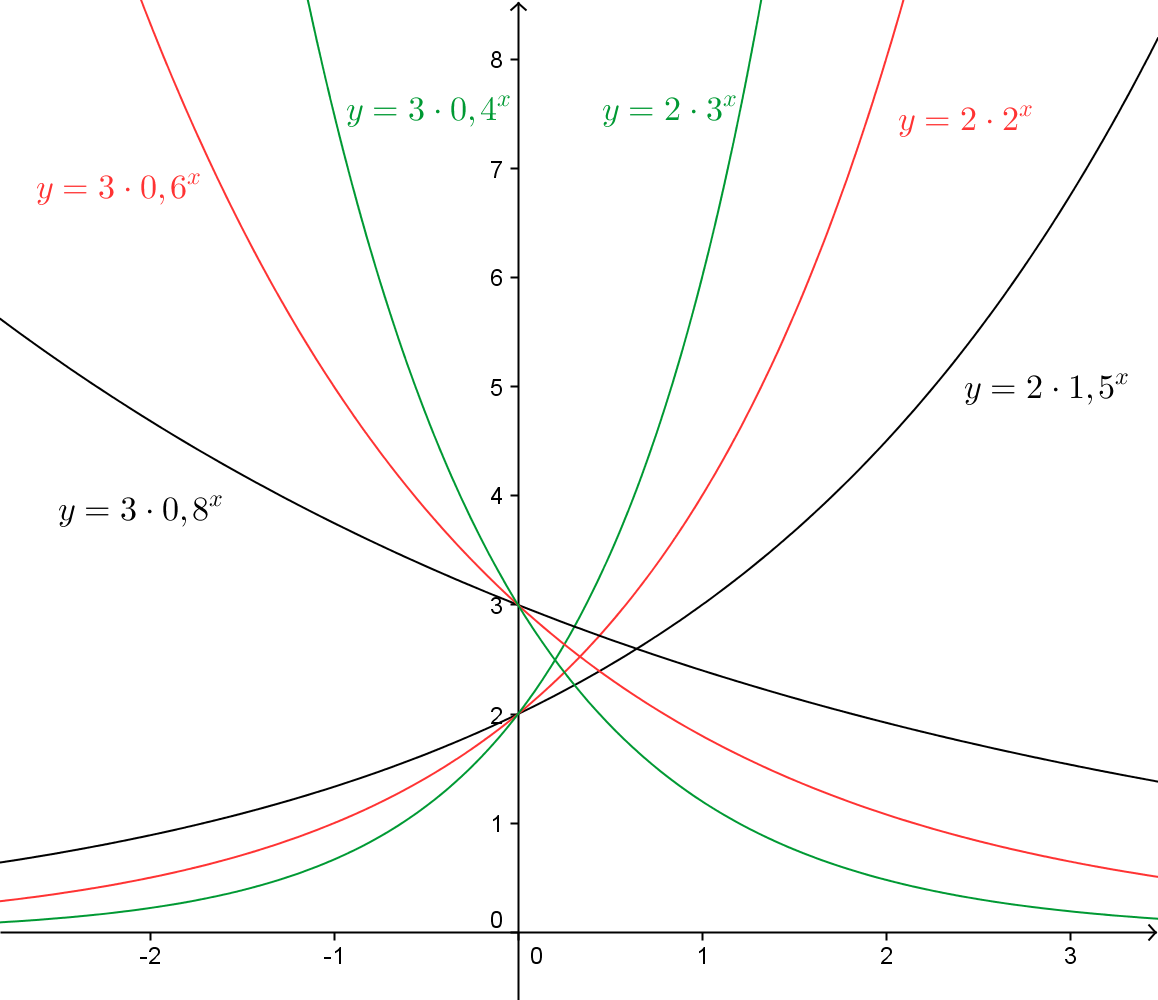
På figuren herunder ses graferne for nogle eksponentielle funktioner.
 |
Her kan du selv undersøge, hvad der sker med grafens udseende, når værdierne af konstanterne a og b ændres (træk i skyderne øverst til venstre)
Beregning af konstanterne a og b
Hvis man kender to punkter kan konstanterne a og b for den eksponentielle funktion, hvis graf går gennem de to punkter, findes ved hjælp af følgende formler
|
Lad der være givet to punkter {$(x_1,y_1)$} og {$(x_2,y_2)$} Konstanten a findes først {$$a=\sqrt[X_2-X_1]{\displaystyle \frac{y_2}{y_1}}$$} Og derefter kan b beregnes ved en af formlerne {$$b=\frac{y_1}{a^{x_1}} \quad eller \quad b=\frac{y_2}{a^{x_2}}$$} |
Bevis
Formlen for a:
De to punkter indsættes i forskriften {$$y_1 = b \cdot a^{x_1} \quad og \quad y_2 = b \cdot a^{x_2}$$} Den sidste ligning divideres med den første {$$\frac{y_2}{y_1} = \frac{b \cdot a^{x_2}}{b \cdot a^{x_1}}$$} b'erne forkortes væk {$$\frac{y_2}{y_1} = \frac{a^{x_2}}{a^{x_1}}$$} Vi bruger en potensregneregel {$$\frac{y_2}{y_1} = a^{x_2-x_1}$$} Endelig findes a ved roduddragning {$$a=\sqrt[X_2-X_1]{\displaystyle \frac{y_2}{y_1}}$$}
Formlerne for b:
Vi bruger udtrykkene, hvor de to punkter er indsat i forskriften {$$y_1 = b \cdot a^{x_1} \quad og \quad y_2 = b \cdot a^{x_2}$$} Og så isoleres b blot i hver formel {$$b=\frac{y_1}{a^{x_1}} \quad eller \quad b=\frac{y_2}{a^{x_2}}$$}
Eksempel
Find forskriften for den eksponentielle funktion, der går gennem punkterne (1,10) og (4,80)
Først findes a {$$a=\sqrt[4-1]{\frac{80}{10}}$$} {$$a=\sqrt[3]{8}$$} {$$a=2$$}
Og dernæst b {$$b=\frac{10}{2^1}$$} {$$b=5$$}
Forskriften er altså {$$f(x) = 5 \cdot 2^x$$}
Vækstform
Eksponentielle funktioner er karakteriseret ved, at en absolut tilvækst i x-værdien giver en relativ (procentvis) ændring af y-værdien. Der gælder nemlig følgende sammenhæng: {$$f(x+\Delta x)=f(x) \cdot a^{\Delta x}$$} Det ses altså, at når x øges med {$\Delta x$} (en absolut tilvækst) ganges y med {$a^{\Delta x}$} (en relativ tilvækst)
Det kan vises på følgende måde:
Bevis
Vi ser på de to punkter {$(x,f(x))$} og {$(x+\Delta x,f(x+\Delta x))$}, som jo ligger på funktionens graf.
Det første punkt indsættes i forskriften
{$$f(x)=b \cdot\ a^x$$}
Det andet punkt indsættes i forskriften
{$$f(x+\Delta x)=b \cdot\ a^{x+\Delta x}$$}
Der bruges en potensregneregel
{$$f(x+\Delta x)=b \cdot\ a^x \cdot a^{\Delta x}$$}
Da {$f(x)=b \cdot\ a^x$} fås
{$$f(x+\Delta x)=f(x) \cdot a^{\Delta x}$$}
Det ses altså, at hvis vi giver x-værdien en absolut tilvækst på {$\Delta x$}, får funktionsværdien en relativ tilvækst (fordi den ganges med et tal), som kan udregnes som {$a^{\Delta x}-1$}.
Eksempel
Lad {$f(x)=3 \cdot 1,2^x$}. Hvis vi lægger fx {$\Delta x = 2$} til x-værdien skal vi altså gange funktionsværdien med {$a^{\Delta x} = 1,2^2 = 1,44$}.
Lad os prøve med x=5 som giver funktionsværdien {$$f(5)=3 \cdot 1,2^5 = 7,46496$$}. Teorien ovenfor siger så, at {$$f(7) = f(5+2) = f(5) \cdot 1,44 = 7,46496 \cdot 1,44 = 10,74954$$}
Læg også mærke til at en tilvækst i x-værdien på 1 ({$ \Delta x =1 $}) medfører, at y-værdien ganges med a, eller med andre ord: hvis vi går 1 ud af x-aksen, ganges y-værdien med a.
Fordoblings- og halveringskonstanter
Eksponentialfunktioner har som nævnt den egenskab, at en bestemt absolut tilvækst på x-aksen giver en bestemt relativ (procentvis) tilvækst på y-aksen, og det omvendte gælder selvfølgelig også, at en bestemt procentvis ændring af y-værdien svarer til en bestemt absolut ændring af x-værdien.
For en voksende eksponentialfunktion svarer en fordobling af y-værdien (en bestemt procentvis tilvækst på 100%) derfor til en bestemt absolut tilvækst i x-værdien. Denne tilvækst kaldes fordoblingskonstanten. For en aftagende eksponentialfunktion gælder tilsvarende, at en halvering af y-værdien svarer til en bestemt, absolut ændring i x-værdien, som kaldes halveringskonstanten
Appletten herunder illustrerer fordoblingskonstanten

Klik for at starte appletten
Fordoblingskonstanten - ofte kaldet {$T_2$} - kan beregnes ved hjælp af formlen
|
{$$T_2 = \frac{log(2)}{log(a)}$$} |
Bevis
Det følger af definitionen på fordoblingskonstanten, at funktionsværdien {$f(x+T_2)$} er det dobbelte af {$f(x)$} {$$f(x+T_2)=2 \cdot f(x)$$} Vi bruger forskriften {$$b \cdot a^{x+T_2} = 2 \cdot b \cdot a^x$$} Og en potensregneregel {$$b \cdot a^x \cdot a^{T_2} = 2 \cdot b \cdot a^x$$} {$b \cdot a^x$} går ud med hinanden {$$a^{T_2} = 2$$} Og så bruger vi logaritmer til at finde {$T_2$} {$$log(a^{T_2}) = log(2)$$} {$$T_2 \cdot log(a) = log(2)$$} {$$T_2 = \frac{log(2)}{log(a)}$$}
For en aftagende funktion findes halveringskonstanten ved hjælp af en tilsvarende formel
|
{$$T_{\frac{1}{2}} = \frac{\displaystyle log(\frac{1}{2})}{log(a)}$$} |
Som også kan vises på helt tilsvarende måde.
Hvis man ønsker at finde konstanten a ud fra en kendt fordoblingskonstant {$T_2$} eller halveringskonstant {$T_\frac{1}{2}$}, kan følgende formler bruges:
|
{$$ a = \sqrt[^{T_2}]{2} \hspace 20pt eller \hspace 20pt a = \sqrt[^{T_\frac{1}{2}}]{\frac{1}{2}}$$} |
Enkeltlogaritmisk koordinatsystem
Eksponentielle funktioner har den egenskab, at deres grafer er rette linjer i et enkeltlogaritmisk koordinatsystem, dvs. et koordinatsystem, hvor y-aksen er logaritmisk, mens x-aksen er normal (ækvidistant). Det følger af denne lille udledning:
{$$y=b\cdot a^x $$} {$$log(y)=log(b\cdot a^x)$$} {$$log(y)=log(b)+x\cdot log(a)$$} {$$log(y)=log(a) \cdot x + log(b)$$}
Da a og b er konstanter er log(a) og log(b) det selvfølgelig også. Lad os sætte a* = log(a) og b* = log(b). Udtrykket ovenfor kan så skrives:
{$$log(y)=a^* \cdot x + b^*$$}
Det ses, at højresiden i ligningen er et lineært udtryk. Det gælder altså for eksponentielle funktioner, at afsættes {$log(y)$} op ad y-aksen og x hen ad x-aksen, bliver grafen en ret linie. Da det at afsætte {$log(y)$} på en normal (ækvidistant) akse svarer til at afsætte y på en logaritmisk akse følger det, at grafen for en eksponentiel funktion er en ret linje i et enkeltlogaritmisk koordinatsystem. Dette er illustreret på figuren herunder

Samme eksponentielle funktion tegnet i et normalt (til venstre) og et enkeltlogaritmisk (til højre) koordinatsystem