Opgaver til optimering

Opgave 1

Af en plade med sidelængderne 40 cm og 50 cm skal der fremstilles en æske uden låg ved at fjerne kvadratiske hjørnestykker og bukke siderne op.

Tegn en skitse af situationen. Kald æskens højde x

Bestem højde, længde og bredde af den æske, som har det størst mulige rumfang, og bestem dette rumfang.

Opgave 2

En kegle har højden h og grundfladeradius r. Keglens overfladeareal – uden bund - kan udregnes som {$\pi \cdot r \cdot \sqrt{r^2 + h^2}$} og dens rumfang som {$\frac{1}{3} \cdot \pi \cdot r^2 \cdot h$}

Bestem dimensionerne af den kegle uden bund, som indeholder 1 liter og har mindst overflade.

Bestem desuden dimensionerne, hvis keglen er med bund

Opgave 3

Et akvarium skal have et volumen på 200 L. Akvariets facade skal have det gyldne snits mål, så bredden skal være 1,618 gange højden. Akvariet skal have bund og sider af glas men ikke noget låg. Bestem akvariets dimensioner, hvis der skal bruges så lidt glas som muligt til fremstillingen.

Opgave 4

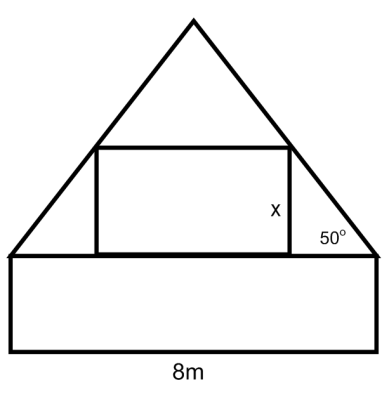
Et parcelhus er 8 m bredt og har en taghældning på {$50^o$} (se skitse herunder). På første sal skal der laves et rektangulært glasparti, som har så stort et areal som muligt, i gavlen. Beregn glaspartiets højde og bredde.