Andengradspolynomier
Et andengradspolynomium er en funktion, som har følgende regneforskrift:
{$$ f(x)=a\cdot x^2 + b\cdot x+c $$}
Hvor a, b og c er konstanter. At polynomiet er af anden grad betyder, at den uafhængige variabel x står i anden potens. Konstanten a skal altså være forskellig fra nul (ellers forsvinder det første led, og der er ikke tale om et andengradspolynomium), mens b og c kan antage alle reelle værdier (og altså også være nul).
Grafen for et polynomium kaldes en parabel. Et eksempel ses herunder:
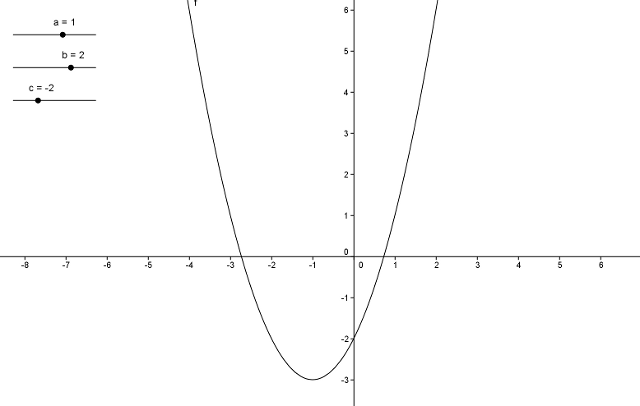
Klik for at starte appletten
Du kan undersøge konstanterne a, b og c's betydning for parablens udseende og beliggenhed ved at justere "skyderne" i appletten.
Som det ses bestemmer a's fortegn, om parablen vender "benene" opad eller nedad. Når a er positiv er parablen "glad", og når a er negativ er parablen "sur".
Det ses også, at c er skæringen med y-aksen (altså f(0)=c)
Parablens toppunkt
Toppunktets koordinatsæt kan beregnes ved hjælp af formlen
|
{$$T= \left( \frac{-b}{2a}, \frac{-d}{4a} \right) $$} hvor d er diskriminanten {$d=b^2-4ac$} |
Bevis
Vi tager udgangspunkt i, at f(0)=c, altså at c er skæringen med y-aksen. Da parablen er symmetrisk omkring en lodret linje, må der derudover være en anden x-værdi, hvor f(x)=c (se figur). Vi finder denne værdi ved at løse ligningen
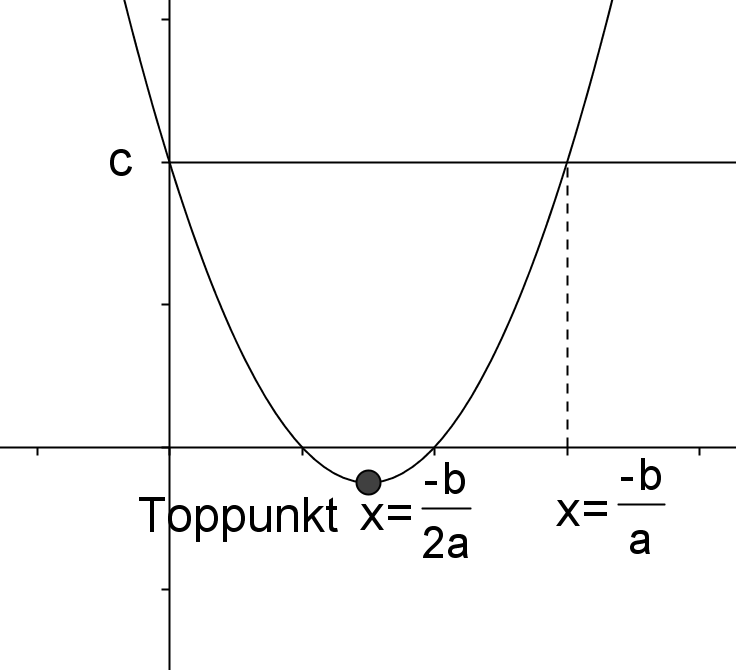
{$$f(x)=c$$} {$$ax^2+bx+c = c$$} {$$ax^2+bx = 0$$} Vi sætter x uden for parentes {$$x(ax+b) = 0$$} Nulreglen giver så {$$x=0 \qquad eller \qquad ax+b = 0$$} Den sidste ligning løses, og vi får {$$x=0 \qquad eller \qquad x = \frac{-b}{a}$$}
Da parablen er symmetrisk må toppunktets x-koordinat ligge midt i mellem de to x-værdier,og den har således værdien {$\displaystyle x = \frac{-b}{2a}$}
Toppunktets y-koordinat findes ved at indsætte det fundne udtryk for x-koordinaten i forskriften:
{$$ y=a \left( \frac{-b}{2a} \right)^2 + b \left( \frac{-b}{2a} \right) +c $$}
{$$ y=a \left( \frac{b^2}{4a^2} \right) - \frac{b^2}{2a} +c$$}
{$$ y=\left( \frac{b^2}{4a} \right) - \frac{b^2}{2a} +c$$}
{$$ y=\left( \frac{b^2}{4a} \right) - \frac{2b^2}{4a} +\frac{4ac}{4a}$$}
{$$ y=\frac{b^2-2b^2+4ac}{4a}$$}
{$$ y=\frac{-b^2+4ac}{4a}$$}
{$$ y=\frac{-d}{4a}$$}
Altså har toppunktet koordinaterne:
{$$T= \left( \frac{-b}{2a}, \frac{-d}{4a} \right) $$}
Som jo var det, vi skulle vise.
Toppunktsformlen kan også bevises ved hjælp af differentialregning
Rødder
Rødderne i et andengradspolynomium f er løsninger til (andengrads)ligningen
{$$ f(x)=0 $$}
eller
{$$ a\cdot x^2 + b\cdot x+c=0 $$}
Rødderne kaldes også for polynomiets nulpunkter. De er x-koordinaterne for parablens skæringspunkter med x-aksen.
Antallet af rødder afhænger af diskriminanten {$d=b^2-4ac$} på følgende måde
|
For d<0 er der ingen rødder For d=0 er der en rod, som findes v.h.a. formlen {$$ \displaystyle x=-\frac{b}{2a}$$} For d>0 er der to rødder, som findes ved formlen {$$ \displaystyle x=\frac{-b\pm \sqrt{d} }{2a} $$} |
Bevis
Vi skal løse ligningen
{$$a\cdot x^2+b\cdot x+c = 0$$}
Først sættes a udenfor parentes
{$$a\cdot (x^2+\frac{b}{a}\cdot x+\frac{c}{a}) = 0$$}
Vi dividerer med a på begge sider og får
{$$x^2+\frac{b}{a}\cdot x+\frac{c}{a} = 0$$}
Så laver vi et lille trick: vi lægger {$ \displaystyle \biggl(\frac{b}{2a}\biggr)^2$} til og trækker det fra igen
{$$x^2+\frac{b}{a}\cdot x+\left(\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2+\frac{c}{a} = 0$$}
Det giver
{$$\left(x+\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2+\frac{c}{a} = 0$$}
Eller
{$$\left(x+\frac{b}{2a}\right)^2-\frac{b^2}{4a^2}+\frac{c}{a} = 0$$}
De sidste to brøker sættes på fælles brøkstreg
{$$\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a^2} = 0$$}
Og flyttes over på den anden side af lighedstegnet
{$$\left(x+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a^2}=\frac{d}{4a^2}$$}
Venstresiden i dette udtryk vil altid være positiv (kvadratet på en størrelse er altid positivt), og derfor har ligningen ingen løsninger, hvis højresiden er negativ. Nævneren i brøken på højre side er også altid positiv, og brøken kan altså kun blive negativ, hvis d er negativ. Heraf følger altså, at ligningen ikke har nogen løsninger, hvis d<0. For {$d\geq0$} kan vi regne videre på følgende måde:
Ligningen {$x^2=c$} har som bekendt to løsninger, nemlig {$\sqrt{c}$} og {$-\sqrt{c}$} (skrives {$x=\pm\sqrt{c}$}) og derfor fås {$$x+\frac{b}{2a}=\pm\sqrt{\frac{d}{4a^2}}$$} Flytter over {$$x=-\frac{b}{2a}\pm\sqrt{\frac{d}{4a^2}}$$} Og omskriver kvadratroden {$$x=-\frac{b}{2a}\pm\frac{\sqrt{d}}{\sqrt{4a^2}}$$} Og {$$x=-\frac{b}{2a}\pm\frac{\sqrt{d}}{2a}$$} Endelig sætter vi på fælles brøkstreg {$$x=\frac{-b\pm\sqrt{d}}{2a}$$} For d=0 reduceres denne formel naturligvis til {$$x=\frac{-b}{2a}$$} Og sætningen er vist.
Faktorisering
Andengradspolynomier kan faktoriseres (skrives som et produkt) på følgende måde:
{$$f(x)=ax^2+bx+c = a(x-r_1)(x-r_2)$$}
hvor {$r_1$} og {$r_2$} er rødder i polynomiet.
Det vises forholdsvis let ved at indsætte formlerne for de to rødder på højresiden ovenfor, gange parenteserne ud og reducere udtrykket, så det bliver lig med venstresiden.
Her gør vi det med et eksempel - det letter udregningerne:
Polynomiet {$$f(x)=2x^2-8x+6$$} har rødderne {$r_1=1$} og {$r_2=3$} og det kan derfor faktoriseres på følgende måde: {$$f(x)=2x^2-8x+6 = 2(x-1)(x-3)$$}
At det har sin rigtighed tjekkes let ved at udregne parentesen på højresiden: {$$2(x-1)(x-3) = 2(x^2-3x-x+3) = 2x^2-8x+6$$}
Bevis
Her ser vi på det rigtige bevis for faktoriseringsformlen
Vi starter med udtrykket {$$a(x-r_1)(x-r_2)$$} som udregnes til {$$a(x^2-x \cdot r_2 - r_1 \cdot x + r_1 \cdot r_2)$$} eller {$$a(x^2 - (r_1+r_2) \cdot x + r_1 \cdot r_2)$$}
Vi omskriver nu de to udtryk {$r_1+r_2$} {$$r_1+r_2 = \frac{-b+\sqrt{d}}{2a} + \frac{-b-\sqrt{d}}{2a} = \frac{-2b}{2a} = -\frac{b}{a}$$} og {$r_1 \cdot r_2$} {$$r_1 \cdot r_2 = \frac{-b+\sqrt{d}}{2a} \cdot \frac{-b-\sqrt{d}}{2a} = \frac{(-b)^2 - (\sqrt{d})^2}{4a^2} = \frac{b^2-(b^2-4ac)}{4a^2} = \frac{c}{a}$$}
De fundne udtryk indsættes i formlen {$$a(x^2 - (r_1+r_2) \cdot x + r_1 \cdot r_2)$$} {$$= a(x^2 - (-\frac{b}{a}) \cdot x + \frac{c}{a})$$} {$$= ax^2+bx+c$$}
Parablens brændpunkt
Det ses af nedenstående figur, at de to parallelle "stråler", som rammer parablen, reflekteres og derefter mødes i punktet E. Ved at aktivere appletten og flytte punkterne A og B ses det, at det gælder for alle stråler, som er parallelle med parablens akse (her y-aksen).
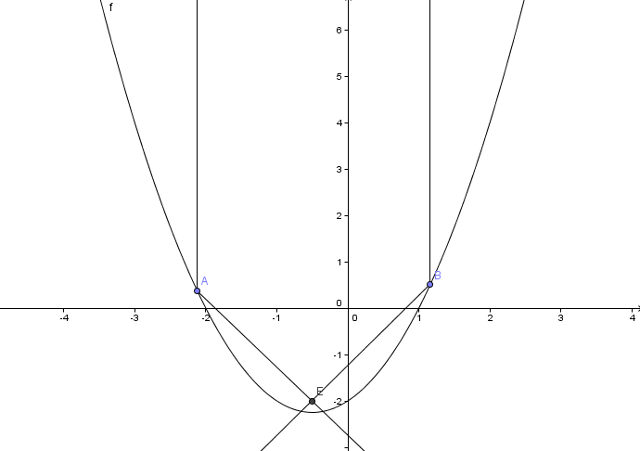
Klik for at starte appletten
Denne egenskab ved parablen udnyttes i parabolantenner, som har form efter en parabel. Radiobølger, der rammer antennen, fokuseres derfor i brændpunktet, hvor selve modtageren er anbragt.